Схемы на резисторах. Делитель напряжения, тока. Электрический расчёт.

5.1 Первый закон Кирхгофа
5.2 Параллельное соединение резисторов. Электрический расчёт.
5.3 Последовательное соединение резисторов. Электрический расчёт.

В предыдущем параграфе, мы находили эквивалентное сопротивление схем, состоящих из нескольких резисторов. Теперь мы посмотрим, что происходит в таких схемах, когда по ним идёт ток.

 

5.1 Первый закон Кирхгофа.

Доброго времени суток, скажу я Вам, уважаемый читатель, и доброго времени года! Хорошо, если за окном лето. И весна — хорошо. Да и осень, вроде, ничего. В принципе, и зима замечательна, если у Вас дома есть батарея централизованного отопления и она горячая. Вот так плавно подвёл я тему разговора к теплосети.

Вас никогда не мучил вопрос, каким же манером фунициклирует отопительная система? А меж тем — всё просто! Где-то, не так далеко, есть котельная. В ней стоит котёл, куча всякой арматуры и теплофикационный насос. Из котельной выходят две водяные трубы. Вернее сказать, одна — выходит, а вторая — заходит. Та, что выходит — с горячей водой, а заходит «обратка» — вода, прошедшая через все батареи и дли-инные трубы системы, и соответственно, уже не горячая. Впрочем, во всём процессе, температура нас интересует менее всего.
Давайте разберёмся, как оно происходит.

Из котельной выходит толстая чугунная труба, по которой течёт горячая вода, только что нагретая в котле. Эта вода называется «прямой», потому что она течёт в «прямом» направлении — то есть, к потребителю. Она течёт, течёт, и приходит в ТЦ — теплоцентр. В ТЦ, эта толстая чугунная труба разделяется на несколько более тонких труб, которые разводятся по домам. К каждому дому идёт по одной «прямой» трубе. В подвале дома труба снова разделяется — на стояки (вертикальные трубы, проходящие через все этажи дома). К каждому стояку на этажах подключены батареи. Вода проходит последовательно через все батареи и доходит до чердака (уже остывшая), где стояки снова сходятся в одну трубу. По этой трубе, вода спускается с чердака и бежит обратно к ТЦ. Теперь вода уже «обратная», поскольку она прошла через батареи потребителя и возвращается обратно в котельную. В ТЦ трубы от разных домов сходятся в одну толстую «обратку», которая уже прямиком идёт в котельную. В котельной, «обратная» вода подаётся на насос, который под давлением нагнетает её в котёл. Далее, из котла, заново нагретая вода снова течёт в систему. Так завершается круговорот воды в отопительной системе.

Как мы увидели, в котельную вернулось ровно столько же воды, сколько и вышло (будем считать, что в системе нигде нет утечек). Из этого можно сделать такие выводы:

1. Сумма потоков воды во всех стояках всех домов равна потоку в «прямой» трубе и равна потоку в «обратной» трубе. Иначе говоря, в любом месте системы суммы всех потоков, имеющих одно направление, будут одинаковыми.
2. В месте разветвления трубы, сумма потоков в отходящих трубах будет равна потоку приходящей трубы.

А теперь перенесём всё сказанное на электрический ток.
Поток воды будет, как всегда, силой тока. Попробуем теперь выразить закон Кирхгофа:

Первый закон Кирхгофа: алгебраическая сумма токов в узле равна «0″, или сумма токов, входящих в узел, равна сумме токов, выходящих из узла.

 

	Узел — это участок схемы, на котором соединяется более двух проводников.

Допустим, в какой то точке соединяется четыре провода. Значит эту точку можно назвать узлом.

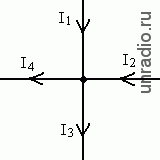
По проводам текут токи. Причём, токи I1, I2 втекают в узел, а токи I3, I4 — вытекают из узла. Значит, по 1-му закону Кирхгофа, можно с уверенностью сказать, что:

I1+I2 = I3+I4

Теперь, зная любые три тока, легко получить четвёртый, сами догадайтесь как.

Но это-то ещё пока просто. Сложности начинаются тогда, когда узел выглядит не как узел, а черт знает как, например:

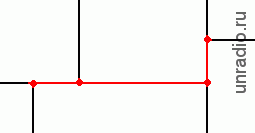
Сколько проводов сходится в таком узле? Правильно, шесть! При этом узлом является кусок схемы, выделенный красным цветом. Ведь, если подумать, все точки, соединенные красным отрезком, можно «подтянуть» друг к другу и сделать одной точкой, в которой будет сходиться 6 проводов. Вот так всё непросто!

Ну ладно, надеюсь, Кирхгофа разрулили. Едем дальше.

 

5.2 Параллельное соединение резисторов. Электрический расчёт.

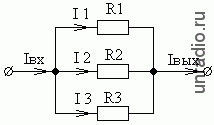
Параллельное соединение резисторов в общем виде выглядит так:

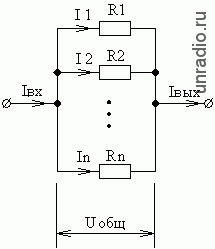
Правила расчёта участка схемы с параллельным соединением резисторов:

1. Общий ток участка схемы равен входному току этого участка, равен выходному току этого участка и равен сумме токов через резисторы:

Iобщ = Iвх =Iвых = I1+ I2+…+ In

2. Напряжения на всех резисторах одинаковы и равны общему:

Uобщ = U1 = U2 = … = Un

Следствия:

1. Чтобы рассчитать общее напряжение, достаточно знать сопротивление любого одного резистора и силу тока, идущего через него.

2. Общий ток можно рассчитать из общего напряжения и эквивалентного сопротивления всех резисторов данного участка.

ЗАДАЧКА: Дана схема: I1 = 2А R1 = 10 Ом R2 = 20 Ом R3 = 40 Ом Найти общий ток Iвх. Решение. Смотрим на схему и думаем: «Ой, ё! А чё делать та-а???». А чё делать — читать, что нам нужно: найти общий ток. Согласно закону Кирхгофа, общий ток Iвх будет равен сумме частных токов I1, I2 и I3. Значит, надо их найти. Величину I1 мы уже знаем, осталось узнать две остальные. А как это сделать? Посмотрим, что нам ещё известно. Ага! R1 = 10 Ом. Значит мы можем вычислить напряжение на резисторе R1: U1 = I1*R1 = 2А * 10 Ом = 20 В. Поскольку все резисторы включены параллельно, то напряжение на каждом из них будет одно и то же, то есть: U1 = U2 = U3 Ну а теперь уже ничего не стоит найти токи I2 и I3: I2 = U2 / R2 = 20 В / 20 Ом = 1 А I3 = U3 / R3 = 20 В / 40 Ом = 0,5 А Ура! Мы на финишной прямой! Осталось только сложить частные токи и получить общий: Iвх = I1 + I2 + I3 = 2 + 1 + 0,5 = 3,5 А Задача решена! Ответ: 3,5 А

Собственно, эта задача настолько хорошо иллюстрирует план расчёта, что мне больше нечего добавить.

И всё-таки, попробуем составить методику расчёта участка с параллельными резисторами.
Методика расчёта примерно такова:

1. Ставим задачу: надо узнать все частные токи (то есть, токи через все параллельные резисторы)
2. Смотрим, что нам дано по условиям задачи.
3. Применяем к данным величинам закон Ома и решаем.

 

http://radiostudy.narod.ru/theory/105voltdevider.htm